“排序算法可以说是数据结构与算法当中最为基础的部分”
概述 排序算法可以说是数据结构与算法当中最为基础的部分,针对的是数组这一数据结构。将数组中的无序数据元素通过算法整理为有序的数据元素即为排序。
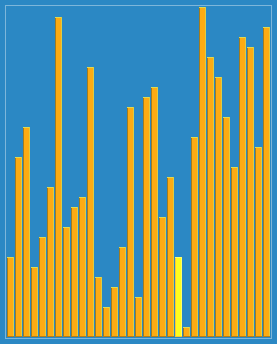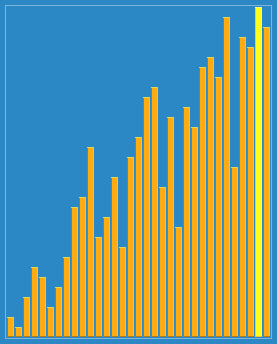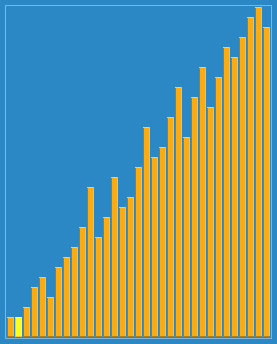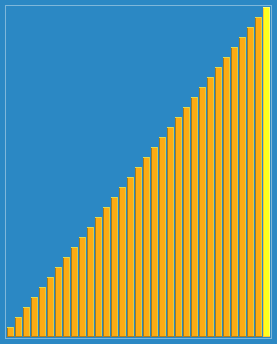
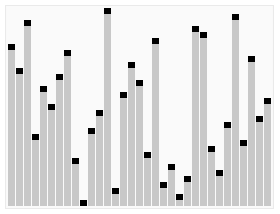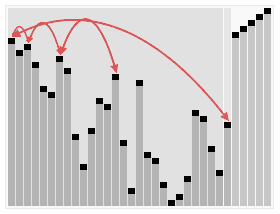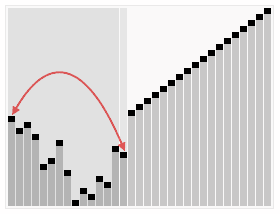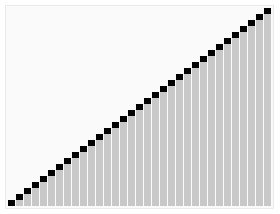
简单排序 冒泡排序 简介:
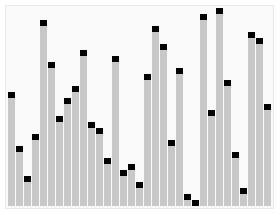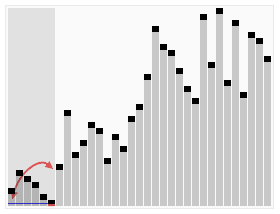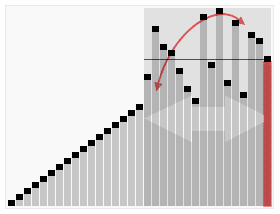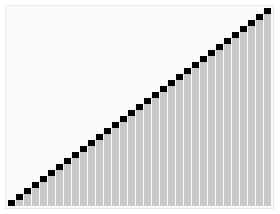
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地访问要排序的数列,将每次访问的最大值“浮”到数组尾部。
步骤如下:
比较相邻的元素。如果第一个比第二个大,就交换他们两个,直到把最大的元素放到数组尾部。
遍历长度减一,对剩下的元素从头重复以上的步骤。
直到没有任何一对数字需要比较时完成。
实现代码:
1 2 3 4 5 def bubbleSort(arr): 1 ]: for j in range(i): if arr[j] > arr[j + 1 ]: swap(arr[j], arr[j + 1 ])
效果图:
选择排序 简介:
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小元素,存放到排序序列的起始位置,重复上述过程,直到所有元素均排序完毕。
步骤如下:
遍历数组,找到最小的元素,将其置于数组起始位置。
从上次最小元素存放的后一个元素开始遍历至数组尾,将最小的元素置于开始处。
重复上述过程,直到元素排序完毕。
实现代码:
1 2 3 4 5 6 7 def selectSort (arr ): for i in range (len (arr)): min = i for j in range (i, len (arr)): if arr[j] < arr[min ]: min = j swap(arr[i], arr[min ])
效果图:
插入排序 简介:
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
步骤如下:
从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果该元素(已排序)大于新元素,将该元素移到下一位置
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置中
重复步骤2
实现代码:
1 2 3 4 5 6 7 8 9 def insertSort(arr): for i in range (len (arr)): tmp = arr[i] pre = i - 1 while pre >= 0 and arr[pre ] > tmp: arr[pre + 1 ] = arr[pre ] pre -= 1 arr[pre + 1 ] = tmp
高级排序 希尔排序 简介:
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
步骤如下:
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;
随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def insertSort(arr): k = 1 while k < len (arr) / 3 : k = 3 * h + 1 //此处为Knuth算法 while k > 0 : for i in range (k , len (arr)): tmp = arr[i] pre = i - k while pre >= 0 and arr[pre ] > tmp: arr[pre + k ] = arr[pre ] pre -= k arr[pre + k ] = tmp k = (k - 1 ) / 3
效果图:
快速排序 简介:
快速排序(Quicksort)是对冒泡排序的一种改进。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
步骤如下:
步骤:
从数列中挑出一个元素,称为 “基准”(pivot),
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def quickSort (arr, low, high) : if low < high: pivot = partition (arr, low, high) quickSort (arr, low, pivot - 1 ) quickSort (arr, pivot + 1 , high) def partition (arr, low, high) : pivot = arr[low] while low < high: while low < high and arr[high] >= pivot: high -= 1 arr[low] = arr[high] while low < high and arr[low] <= pivot: low += 1 arr[high] = arr[low] arr[low] = pivot return low
效果图:
归并排序 简介:
归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
步骤如下:
申请空间,创建两个数组,长度分别为两个有序数组的长度
设定两个指针,最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 def mergeSort(arr, low, high): if low < high: mid = low + (high - low) / 2 mergeSort(arr, low, mid ) mergeSort(arr, mid + 1 , high) return merge (arr, low, mid , high) def merge (arr, low, mid , high): leftArr = arr[low : mid + 1 ] rightArr = arr[mid + 1 : high + 1 ] i, j, m = 0 , 0 , low while i < len (leftArr) and j < len (rightArr): if leftArr[i] < rightArr[j]: arr[m] = leftArr[i] i += 1 else : arr[m] = rightArr[j] j += 1 m += 1 while i < len (leftArr): arr[m] = leftArr[i] m += 1 i += 1 while j < len (rightArr): arr[m] = rightArr[j] m += 1 j += 1
实现效果:
堆排序 简介:
堆积排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
步骤如下:
按堆的定义将数组R[0..n]调整为堆(这个过程称为创建初始堆),交换R[0]和R[n];
将R[0..n-1]调整为堆,交换R[0]和R[n-1];
重复上述过程,直到交换了R[0]和R[1]为止。
实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def heapSort(arr): for i in range(len(arr) / 2 )[::-1 ]: heapAdjust (arr, i, len(arr)) for i in range(len(arr) - 1 )[::-1 ]: swap (arr[i], arr[0 ]) heapAdjust (arr, 0 , i) def heapAdjust(arr, parent, length): tmp = arr[parent] child = 2 * parent + 1 while child < length: if child + 1 < length and arr[child + 1 ] > arr[child]: child += 1 if arr[child] <= tmp: break arr [parent] = arr[child] parent = child child = 2 * parent + 1 arr [parent] = tmp
效果图:
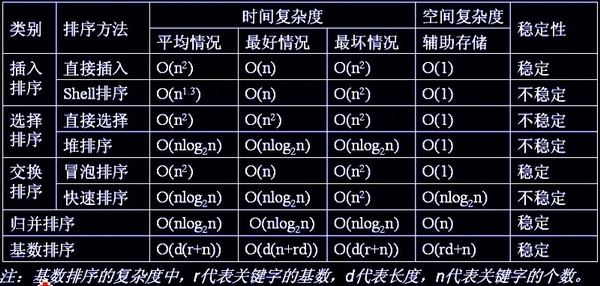
各排序算法时间空间复杂度